Contents - introduction - Prerequistits - Skeleton - Methods for dimension reduction - Agglomeration - Model hyper-parameterization - Principal Component Analysis (PCA) - Resources
introduction
In earlier posts in this series on machine learning, you have applied both linear and non-linear regressors for predictive modelling. In the post on feature selection different methods for discriminating among the independent features aiming at retaining only the most adequate is applied. In this post you will instead rearrange the independent variables and create a novel set of independent variables reducing the dimensionality (number of columns) while retaining more of the variation. The methods presented in this post are considered more powerful than simply discriminating among the independent variables.
You can copy and paste the code in the post, but you might have to edit some parts: indentations does not always line up, quotations marks can be of different kinds and are not always correct when published/printed as html text, and the same also happens with underscores and slashes.
The complete code is also available here.
Prerequistits
The prerequisites are the same as in the previous posts in this series: a Python environment with numpy, pandas, sklearn (Scikit learn) and matplotlib installed.
Module Skeleton
The module skeleton code is under the button.
Methods for dimension reduction
This post covers two different methods for reducing the dimensions in the independent variables:
- Feature agglomeration
- Principle Component Analysis (PCA)
Import the required packages from Scikit learn.
from sklearn.cluster import FeatureAgglomeration
from sklearn.decomposition import PCA
For the feature agglomeration you are going to use a pipeline approach for setting up a selection model, and then sending the model to the grid search module GridSearchCV that you used in the previous post. For that you also need to import the Scikit learn modules for BayesianRidge (the model to use for agglomeration), Pipeline and Memory. And then you also need to import GridSearchCV and RandomizedSearchCV.
from sklearn.linear_model import BayesianRidge
from sklearn.pipeline import Pipeline
from sklearn.externals.joblib import Memory
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import RandomizedSearchCV
Agglomeration
Agglomeration aims at reducing the dimensionality (number of columns) of the independent (X) data by merging features that show similar variation patterns. The clustering function in Scikit learn FeatureAgglomeration uses the Ward hierarchical cluster analysis, and clusters the original X dimension to n_clusters. Add the function WardClustering to the RegressionsModels class.
def WardClustering(self, nClusters):
ward = FeatureAgglomeration(n_clusters=nClusters)
#fit the clusters
ward.fit(self.X, self.y)
#print out the clustering
print 'labels_', ward.labels_
#Reset self.X
self.X = ward.transform(self.X)
#print the shape of reduced X data
print 'Agglomerated X data shape:',self.X.shape
The function resets the class X (self.X) variable, and all subsequent processing (regression modelling) will use the clustered data instead of the original data. Your models will then have fewer independent features to sieve through. The modelling will thus be faster, but with only a small loss in predictive power, and without redundancy among the independent features.
When calling the WardClustering function you have to give the number of clusters you want to merge the original dataset into. To use the function, call it from the __main__ section.
nClusters = 5
regmods.WardClustering(nClusters)
#Processes called after the clustering will use the clustered X dataset for modelling
#Setup regressors to test
regmods.modD['KnnRegr'] = {}
regmods.modD['DecTreeRegr'] = {}
regmods.modD['SVR'] = {}
regmods.modD['RandForRegr'] = {}
#Invoke the models
regmods.ModelSelectSet()
#set the random tuning parameters
regmods.RandomTuningParams()
#Run the tuning
regmods.RandomTuning()
#Reset the models with the tuned hyper-parameters
regmods.ModelSelectSet()
#Run the models
regmods.RegrModTrainTest()
regmods.RegrModKFold()
With the __main__ section set as above the module:
- agglomerates the X data to 5 clusters,
- sets up 4 regressors (‘KnnRegr, ‘DecTreeRegr’, ‘SVR’ and ‘RandForRegr’),
- uses a randomized tuning for setting the model hyper-paramters for each regressor, and
- test the predictive powers of each regressor using both train+test and cross validation.
It will take a while.
Tuning the number of clusters
In the section above we set an arbitrary number (5) defining the number of clusters that we wanted our dataset to be merged into. To tune an optimal number of clusters we could (manually) change the parameter nClusters and check the result for each trial. But it would be much better to set up a process using a grid search evaluating different alternative agglomerations. In the previous post you used GridSearchCV for finding the best hyper-parameters. GridSearchCV can also be used for identifying the optimal number of clusters. But you must set it up so that GridSearchCV has some criterion on which to base the search for the optimal nClusters.
What is needed for tuning the optimal number of clusters is an estimator (regressor) that evaluates the effects of different nClusters. You thus need a process that:
- iteratively changes nClusters,
- agglomerates X into nClusters using WardClustering,
- sends the clustered X dataset to an estimator, and
- evaluates the results from the estimator.
In Scikit learn this can be setup using a pipeline (Pipeline) and GridSearchCV. Pipeline defines the functions to link, and GridSearchCV defines the cluster sizes to test and iterates the process. The example below uses the Bayesian linear regressor as the estimator, and is taken from a Scikit learn page on Feature agglomeration.
def TuneWardClustering(self, nClustersL, kfolds=2):
print 'Cluster agglomereations to test',nClustersL
cv = KFold(kfolds) # cross-validation generator for model selection
ridge = BayesianRidge()
cachedir = tempfile.mkdtemp()
mem = Memory(cachedir=cachedir)
ward = FeatureAgglomeration(n_clusters=6, memory=mem)
clf = Pipeline([('ward', ward), ('ridge', ridge)])
# Select the optimal number of parcels with grid search
clf = GridSearchCV(clf, {'ward__n_clusters': nClustersL}, n_jobs=1, cv=cv)
clf.fit(self.X, self.y) # set the best parameters
print 'initial Clusters',iniClusters
#report the top three results
self.ReportSearch(clf.cv_results_,3)
#rerun with the best cluster agglomeration result
return (clf.best_params_['ward__n_clusters'])
The function TuneWardClustering requires a list (nClustersL) containing the sizes of the clusters you want to test (for example, to test clustering the X data to between 4 and 10 cluster, the list would be [4,5,6,7,8,9,10]). You can also set the number of folds (kfolds) to use in the cross validation. The function returns a single number, the number of clusters that resulted in the highest score.
You then also need to add the reporting function for the results of the pipeline clustering.
def ReportSearch(self, results, n_top=3):
for i in range(1, n_top + 1):
candidates = np.flatnonzero(results['rank_test_score'] == i)
for candidate in candidates:
print("Model with rank: {0}".format(i))
print("Mean validation score: {0:.3f} (std: {1:.3f})".format(
results['mean_test_score'][candidate],
results['std_test_score'][candidate]))
print("Parameters: {0}".format(results['params'][candidate]))
print("")
When running the module you can choose to explore the results, or you can just send the best clustering results (the returned parameter from TuneWardClustering) to the function WardClustering.
To test the agglomeration function for exploring the results of the feature agglomeration, update the __main__ section.
#nClusters = 5
#Agglomerate the X data
nClustersL = [4,5,6,7,8,9,10,11]
nClusters = regmods.TuneWardClustering(nClustersL)
regmods.WardClustering(nClusters)
'''
#Processes called after the clustering will use the clustered X dataset for modelling
#Setup regressors to test
regmods.modD['KnnRegr'] = {}
regmods.modD['DecTreeRegr'] = {}
regmods.modD['SVR'] = {}
regmods.modD['RandForRegr'] = {}
#Invoke the models
regmods.ModelSelectSet()
#set the random tuning parameters
regmods.RandomTuningParams()
#Run the tuning
regmods.RandomTuning()
#Reset the models with the tuned hyper-parameters
regmods.ModelSelectSet()
#Run the models
regmods.RegrModTrainTest()
regmods.RegrModKFold()
'''
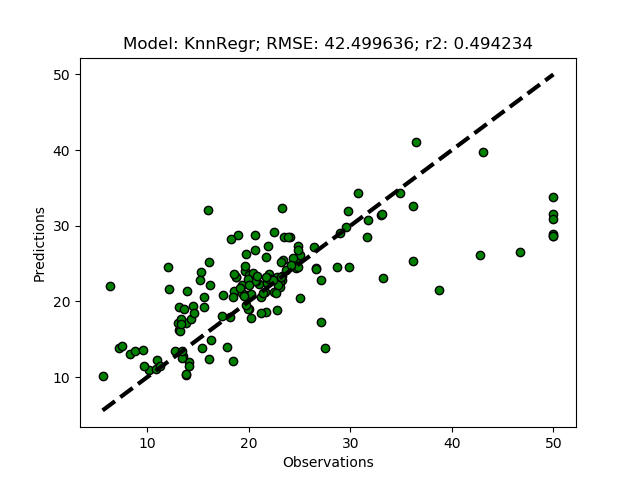
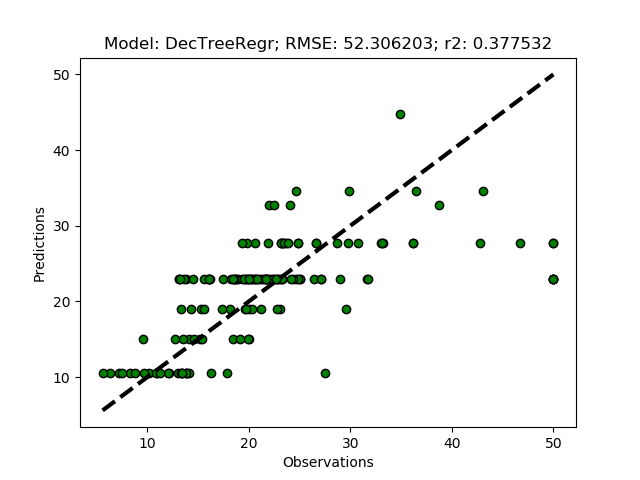
If you kept the suggested parameters, the results should be that the best option is to use 6 clusters.
Model with rank: 1
Mean validation score: 0.441 (std: 0.100)
Parameters: {'ward__n_clusters': 6}
Model with rank: 2
Mean validation score: 0.435 (std: 0.029)
Parameters: {'ward__n_clusters': 9}
Model with rank: 3
Mean validation score: 0.415 (std: 0.075)
Parameters: {'ward__n_clusters': 7}
To run the models with the suggested number of clusters, just remove the commented section invoking the models (the triple quotations '''). The module then runs both the training+test model predictions RegrModTrainTest) and the folded cross validation predictions RegrModKFold). All models are tuned before actually running the predictions, hence it will take a while for the model formulations to finish and the first plot to appear.
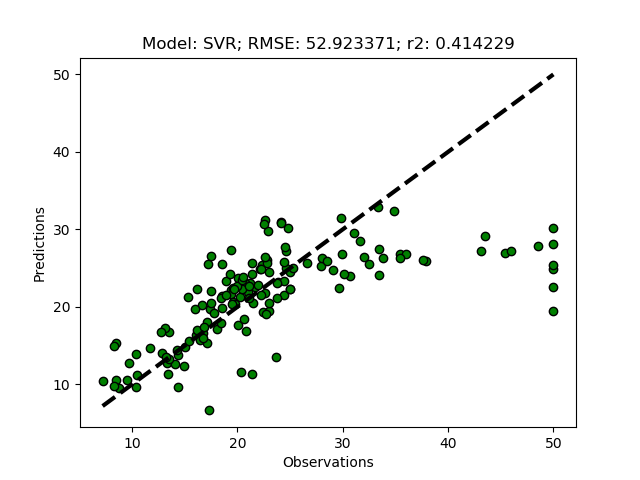
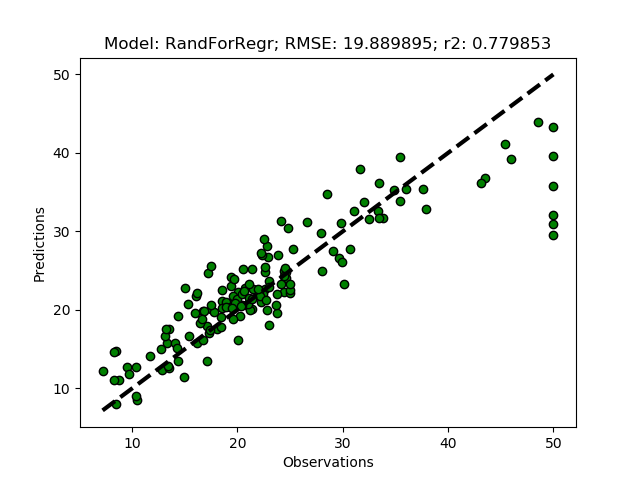
Principal Component Analysis (PCA)
PCA is a linear transformation that places a set of n-vectors (called eigen-vectors) sequentially oriented orthogonally with regard to previously defined vectors, while seeking an orientation that maximizes the explanation of the remaining variation. The maximum number of vectors that can be constructed equals the number of input features, whereafter all the variation in the original data is explained by the vectors. The information content decreases with each vector, and usually the 3 to 4 first components carry almost all information from the original dataset.
You already imported the PCA function from Scikit learn above, to implement the PCA dimension reduction add the function PCAdecompose to the RegressionModels class.
def PCAdecompose(self, minExplainRatio=0, nComps=3 ):
if minExplainRatio > 0:
pca = PCA()
pca.fit(self.X)
print 'PCA explained ratios', pca.explained_variance_ratio_
nComps = len([item for item in pca.explained_variance_ratio_ if item >= minExplainRatio])
print 'accepted components: %(n)d' %{'n':nComps}
pca = PCA(n_components=nComps)
pca.fit(self.X)
self.X = pca.transform(self.X)
print 'PCA explained ratios', pca.explained_variance_ratio_
print 'PCA X data shape:',self.X.shape
By default PCAdecompose reduces the input array to three principal components. Alternatively you can either set a threshold for the ratio of the total variation that a component must explain to be accepted (minExplainRatio), or set the number of components to be constructed (nComps). For the latter to be used, you must set the former to zero (0). To run your regressors using eigen-vectors from PCA as the independent variables, just replace the agglomeration with PCA in the __main__ section.
'''
#Agglomerate the X data
nClustersL = [4,5,6,7,8,9,10,11]
nFeatures = regmods.TuneWardClustering(nClustersL)
regmods.WardClustering(nClusters)
'''
#Dimension reduction using PCA
nFeatures = regmods.PCAdecompose() #default: produces 3 eigen-vectors
#nFeatures = regmods.PCAdecompose(0.1) #produces all eigen-vectors that explain at least 10% of the total variation
#nFeatures = regmods.PCAdecompose(0, 4) #produces 4 eigen-vectors
#Setup regressors to test
regmods.modD['KnnRegr'] = {}
regmods.modD['DecTreeRegr'] = {}
regmods.modD['SVR'] = {}
regmods.modD['RandForRegr'] = {}
#Invoke the models
regmods.ModelSelectSet()
#set the random tuning parameters
regmods.RandomTuningParams(nFeatures)
#Run the tuning
regmods.RandomTuning()
#Reset the models with the tuned hyper-parameters
regmods.ModelSelectSet()
#report model settings
regmods.ReportModParams()
#Run the models
regmods.RegrModTrainTest()
regmods.RegrModKFold()
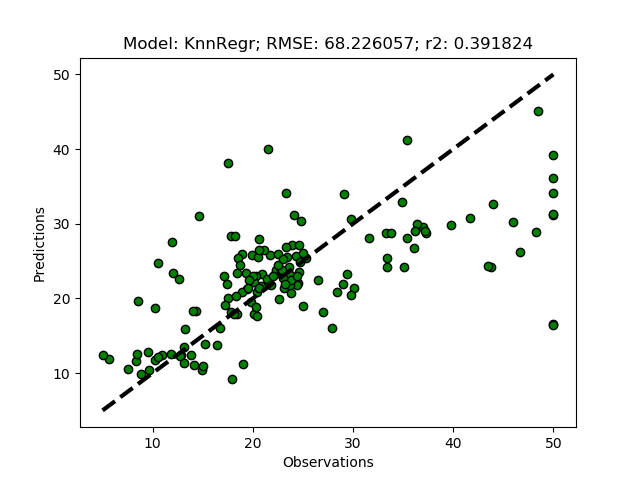
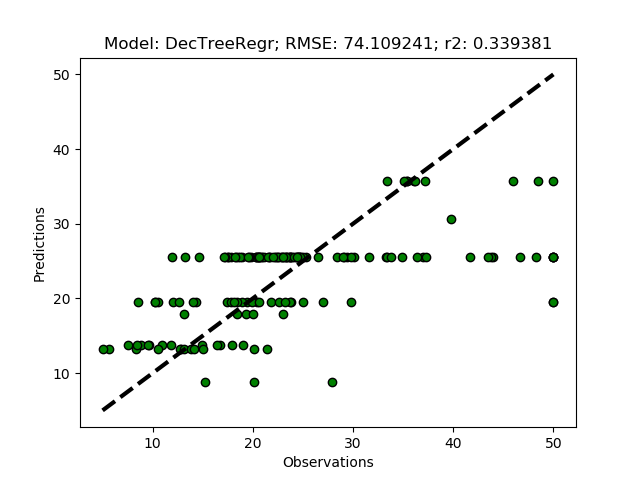
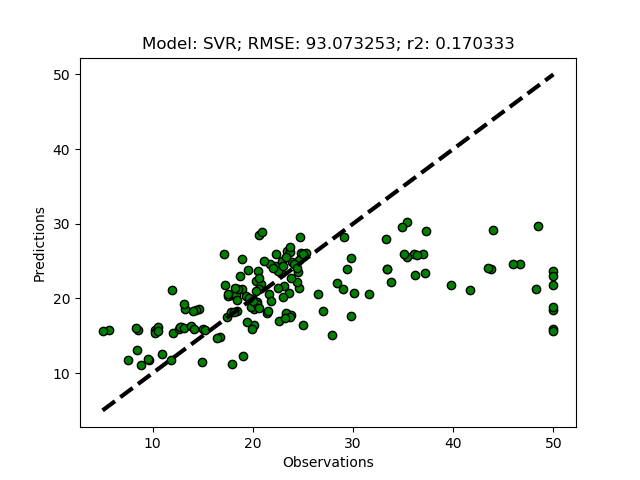
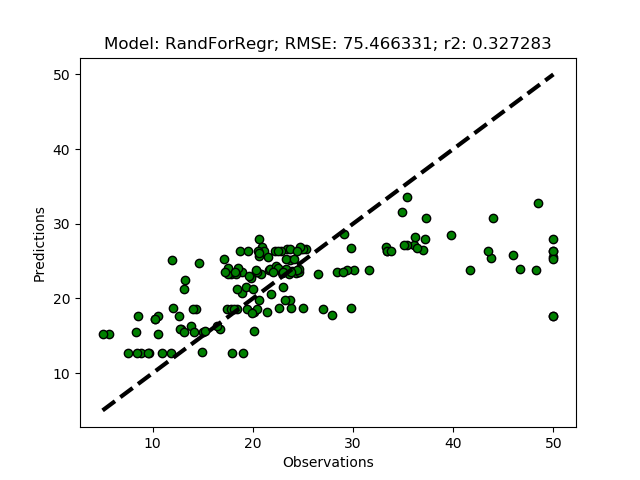
The complete code of the module that you created in this post is available at GitHub.
Resources
Unsupervised dimensionality reduction, Scikit learn.
FeatureAgglomeration, Scikit learn.
Decomposing signals in components, Scikit learn.
PCA, Scikit learn.
Completed python module on GitHub.